Riješi nejednadžbe:

\[\frac{3^{2x+1}-4\cdot 3^x+1}{3^x-9^x}\leq 0\]

\textbf{Rješenje:1) }Na lijevoj strani nejednadžbe je razlomak, a on nije definiran za vrijednosti nepoznanice za koje je nazivnik nula. Jednadžba će imati smisla za\[3^x-9^x\neq 0\Rightarrow 3^x\neq 3^{2x}\Rightarrow x\neq 0.\] Uočiti \(3^{2x+1}=\left(3^x\right)^2\cdot 3\) i \(9^x=\left(3^x\right)^2\) što nakon zamjene \(3^x=t\) daje nejednadžbu \[\frac{3t^2-4t+1}{t-t^2}\leq 0\] U brojniku i nazivniku su kvadratne funkcije po nepoznatoj \(t\) i problem ćemo riješiti geometrijski. Nacrtati ćemo u istom koordinatnom sustavu obje parabole s tim što trebamo točke presjeka s x-osom (nultočke) i okrenutost parabole. Za brojnik je \[t_{1,2}=\frac{4\pm 2}{6}\Rightarrow t_1=\frac 13,t_2=1\] i okrenuta je otvorom prema gore, a u nazivniku je\[t(1-t)=0\Rightarrow t_1=0,t_2=1\] i okrenuta je otvorom prema dole.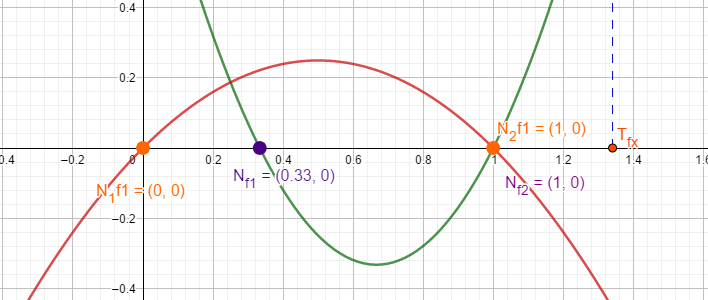
Rješenje je \(t<0,t\geq \frac 13, t\neq 1\). Povratak u zamjenu daje:
\[3^x<0,\:3^x\geq \frac 13,\: 3^x\neq 1\]
Prvi uvjet je uvijek ispunjen (\(3^x>0\) za svaki \(x\)), dok druga dva daju konačno rješenje
\[x\geq -1,x\neq 0\].

Rješenje je: \(\color{red}{x\geq -1,x\neq 0.\clubsuit}\).