\(\textbf{Zadatak 4. }\) Analiziraj i nacrtaj graf kvadratne funkcije \(f(x)=x^{2}+2x-3.\)
\(\textbf{Rješenje:}\)
\(\textbf{1) }\) Područje definicije kvadratne funkcije je \(D_f=R.\)
\(\textbf{2) }\) \(a=1>0\) parabola je okrenuta otvorom prema gore.
\(\textbf{3) }\) Tjeme
\[x_0=\dfrac{b}{2a}=\frac{2}{2}=-1\]
\[ y_0=\dfrac{4ac-b^2}{4a}=-\dfrac{-12-4}{4}=-4\]
\[\text{Tjeme je u točki }T(-1,-4).\]
\(\textbf{4) }\)Ekstrem
\(a=1>0\) funkcija ima minimalni vrijednost (minimum), i vrijedi
\[y_{min}=f(-1)=-4.\]
\(\textbf{5) }\) Tijek funkcije,
| \(x\) | \(-\varpropto\) | \(\nearrow\) | \(-1\) | \(\nearrow\) | \(+\varpropto\) |
| \(f(x)\) | \(+\varpropto\) | \(\searrow\) | \(-4\) | \(\nearrow\) | \(+\varpropto\) |
\(\textbf{6) }\) Presjeci s koordinatnim osimaresjek
\((0,-3)\) - presjek s \(y-osom.\)
\[x_{1,2}=\dfrac{-2\pm\sqrt{16}}{2}=\dfrac{-2\pm 4}{2}.\]
\[x_1=-3,\:\:x_2=1\]
Nultočke su \((-3,0),(1,0).\)
\(\textbf{7) }\) Parabola
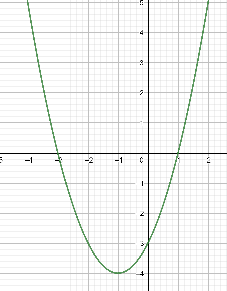
\(\textbf{8) }\) Znal funkcije
\[f(x)\geq 0\:\:\:\:\text{ za }\:\:\:\:x\in\left<-\varpropto,-3\right]\cup\left[1,+\varpropto\right>;\]
\[f(x)<0\:\:\:\:\text{ za }\:\:\:\:x\in\left<-3,1\right>.;\]
