Vrhovi su trokuta \(A(-2,3),B(4,-5)\quad C(-3,1)\). Odredi jednadžbe pravaca na kojima leže visin tog trokuta. 

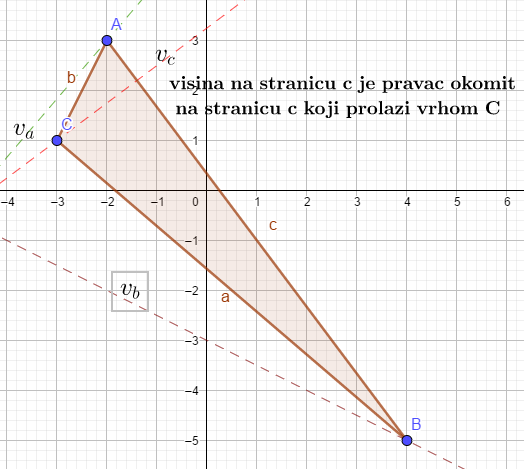
\(\textbf{Rješenje:}\quad\)Visina trokuta je okomica na stranicu trokuta kroz naspramni vrh toj stranici. Ja ću odrediti visinu na stranicu \(c\) određenu vrhovima \(A\:i\:B\). Kao i u zadatku 8, trebam pravac koji sadrži stranicu \(c\), vrijedi

\begin{gather*}y-y_A=\frac{y_B-y_A}{x_B-x_A}(x-x_A)\\y-3=\frac{-5-3}{4+2}(x+2)\\y=\frac{-8}{6}(x+1)+3\\y=\frac{-4}{3}x+\frac{1}{3}\end{gather*}

Koeficijent smjera pravca \(c\cdots y=\frac{-4}{3}x+\frac{1}{3}\) je \(a_c=\frac{-4}{3}\). Zbog okomitosti je koeficijent smjera simetrale koji sadrži visinu \(v_c\) dat s

\[a_{v_c}=-\frac{1}{a_c}=-\frac{1}{\frac{-4}{3}}=\frac 34.\]

Visina \(v_c\) prolazi točkom \(C\) i ima koeficijent smjera \(v_c=\frac 34\) te joj je jednadžba

\begin{gather*}y-y_C=a_{v_c}(x-x_C)\\y-1=\frac34(x+3)\\y=\frac34 x+\frac94+1\\y=\frac 34 x+\frac{13}{4}\end{gather*}

Konačno, jednadžba visine na stranicu \(c\) je

\[v_c\ldots y=\frac 34 x+\frac{13}{4}\].