Riješi logaritamske nejednadžbe:

 \[\log\frac{10}{x}\cdot \log(10x)\geq \log\frac{1}{10x}\]

\(\textbf{Rješenje:1) }\) Zbog podrućja defincije logaritama mora veijediti \(10x>0,\frac{10}{x}>0\:i\:\frac{1}{10x}>0\) i sva tri su ispunjena za \(x>0\). Koristeći svojstva logaritama malo ćemo preurediti jednadžbu
\begin{gather*}
\log\frac{10}{x}\cdot \log(10x)\geq \log\frac{1}{10x}\\\left(\log 10-\log x\right)\cdot\left(\log 10+\log x\right)\geq \log 1-\left(\log 10+\log x\right)
\end{gather*}
Zbog \(\log 1=0,\:\log 10=1\) iamo jednadžbu \[\left(1-\log x\right)\cdot\left(1+\log x\right)\geq -1-\log x\]
odnosno \[1-\log^2 x+\log x+1\geq 0\] Množenje s \(-1\) i sređivanje daje kvadratnu jednadžbu po \(\log x\)
\[\log^2 x -log x-2\leq 0\]
Zamjena \(\log x=t\) daje nejednadžbu
\[t^2-t-2\leq 0\]
Lijeva strana je kvadratna funkcija po t kojau presjeca x-os u točkama \(t_{1,2}=\frac{1\pm 3}{2} \Rightarrow t_1=-1,t_2=2\) i okrenuta je prema gore.

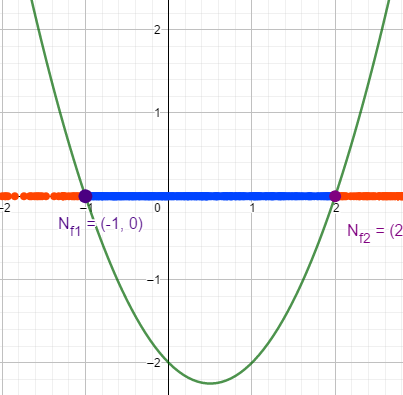
Manja ili jednaka nuli je za \[-1\leq t\leq 2\] što nakon povrata u zamjenu daje \[-1\leq \log x\leq 2\]
\[\log 0.1\leq \log x\leq \log 100\] Rješenj jednadžbe je
\[0.1\leq x\leq 100.\color{red}{\clubsuit}\]

Rješenje je: \(\color{red}{0.1\leq x\leq 100.\clubsuit}\).