Neka je u ravnini \(\pi\) zadan konveksan mnogokut \(A_1A_2\ldots A_n\). S \(B\) ćemo označavati sam mnogokut,  kao i mjerni broj njegove površine. Data je dužina \(\overline{MN}\)  koja ne leži u toj ravnini i koju nazivamo izvodnica.

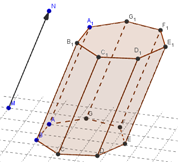
Skup točaka ravnine \(\pi\) koje pripadaju dužinama \(\overline{PP'}\) paralelnim i sukladnim izvodnici \(\overline{MN}\) pri čemu točka \(P\) prolazi svim točkama mnogokuta \(B\) nazivamo prizma.

Sastavnica prizme

• Mnogokut \(B\) nazivamo osnovka ili baza prizne. Prizma ima dvije baze, donju i gornju.
• Stranice na osnovkama nazivaju se osnovni bridovi prizme,
• spojnice odgovarajućih vrhova donje i gornje osnovke nazivamo bočni bridovi prizme,
• Paralelogrami \(A_1A_2A_1'A_2'\), \(A_2A_3A_2'A_3'\) itd. nazivaju se bočne strane ili pobočke prizme. Sve bočne strane prizme čini pobočje prizme.
• Visina prizme \(v\) predstavlja udaljenost ravnina u kojima leže baze prizme.

  Klasifikacija prizmi 

• Ako je baza prizme trokut za prizmu kažemo da je trostrana, četverokut četverostrana i općenito n-terokut za prizmu kažemo da je n-treostrana.
• Prizma je uspravna ako je izvodnica okomita na ravninu osnovke.
• Prizma je pravilna ako je uspravna i ako joj jeosnovka pravilan n-terokut.

Prizma je konveksan poliedar. Ravnine donje i gornje osnovke su paralelne. Ravnine bočnih strana prizme paralelne su izvodnici prizme. Ako prizma nije uspravna tada kažemo da je kosa.